A bond future is a derivative security that supplies the risk exposure of a particular bond without the need to hold that physical security. In other words, it provides the effective exposure of a bond without the market exposure. To illustrate what this means, consider the following examples.

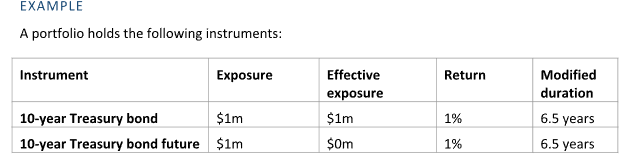
The return of the portfolio is given by

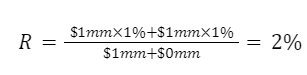
The modified duration of the portfolio is given by

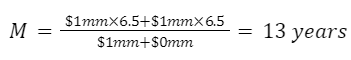
The inclusion of the bond future has leveraged the return and risk of the portfolio. In this case, the return and the modified duration are doubled.

The CTD

Most bond futures are traded using standard contracts. For instance, 3 and 10 year Treasury bond futures are widely used in the US. 

The underlying physical bond that is delivered when the contract expires will vary according to market conditions. This bond is called the cheapest to deliver (or CTD) and is selected from a list of five or six that are set up when the futures contract is issued.

There are numerous technical details underpinning the relationship between a futures contract and its underlying security. However, for FIA’s purposes all you need to know are the characteristics of the current CTD bond for that contract (and its risk numbers, if you are using the perturbational model). The futures contract in the security master table is set up using this bond’s maturity and coupon.

The CTD bond can change over the lifetime of a futures contract, so it is worthwhile monitoring on the DLV page in Bloomberg. If the CTD does change, this can be modelled in FIA by using the effective date functionality.

The exception are constant maturity futures, which are traded in Australia and New Zealand. These are treated separately below.

The cash offset

A bond future generates the risk and return of its underlying bond, but without the exposure. One way to model this is to treat the future as having two legs:

• A bond leg
• A cash offset leg, with equal and opposite market exposure to the bond leg.

Setting up a bond future

Summarising, a bond future such as a 10 year bond contract is set up as follows:

• A holding in the CTD bond
• An equal but opposite cash holding, called the cash offset

Note that the cash offset is merely an accounting convenience that allows us to model the zero market exposure feature of a bond futures contract. It should be kept separate from other physical cash holdings in the portfolio, and does not generate interest.

Working without cash offsets

FIA offers an alternative route to the cash offset approach when modelling bond futures. If required, the futures contract can be modelled as a one-leg security without the need to supply a cash offset.

To do this, set up the bond future using the same characteristics as the CTD bond, but set the effective exposure flag in the future’s security definition to zero (its default value is one). FIA’s risk and returns reports will then give the same results as if a cash offset had been supplied, but without the appearance of that offset in the portfolio’s holdings reports.

First-principles modelling of bond futures

First principles modelling of bond futures does not require that daily risk numbers (yield, modified duration) need be supplied. Instead, FIA calculates the risk characteristics of the bond internally. This approach requires that a pricing function and the CTD’s parameters (maturity date, coupon, coupon frequency) be supplied in the security master file.

Perturbational modelling of bond futures

To model a bond future using the perturbational approach, ensure no pricing function specified in the security’s master record, and supply yield and modified duration data in the weights and returns file for all dates on which the future is held. 

Constant maturity futures

In some countries, bond futures contracts are cash settled, rather than having a particular bond delivered at contract expiration. Futures contracts are issued on a nominal security with a maturity date that is always a fixed number of years ahead of the current settlement date. 

This would be cumbersome to model using the standard bond pricing approach, as the security’s maturity date would have to be reset each day. For these asset types, FIA therefore provides custom pricing functions (FT_AUD_3_YEAR_BOND_FUTURE, FT_AUD_10_YEAR_BOND_FUTURE) which can be used to model such asset types. Coupon, maturity and frequency are all specified within the pricing function, so there is no need to specify these quantities when using these functions. 

Modelling carry for bond futures

Carry is usually defined as the return generated by the passage of time. For bond futures, this can be calculated as the yield of the CTD bond, minus the relevant funding rate, times the interval as a fraction of a year. 

However, one can argue that as the future does not accrue any income until delivery, its carry should be zero.

FIA does not attempt to provide a definitive answer to this issue. Instead, the program allows the user to input whatever yield is appropriate in column 6 of the weights and returns file. This value will then override any internally calculated value. 

Examples

The following four examples illustrate various ways in which a simple portfolio containing a bond future can be set up in FIA.  Data files are available from Flametree upon request, together with configuration settings and a simple yield curve file, which are the same for all four examples. 

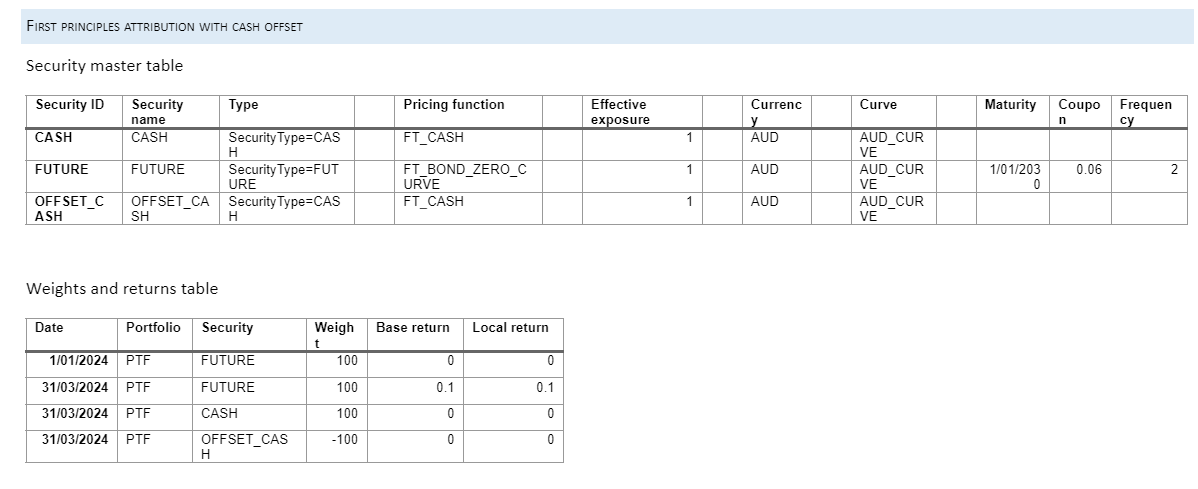
Notes

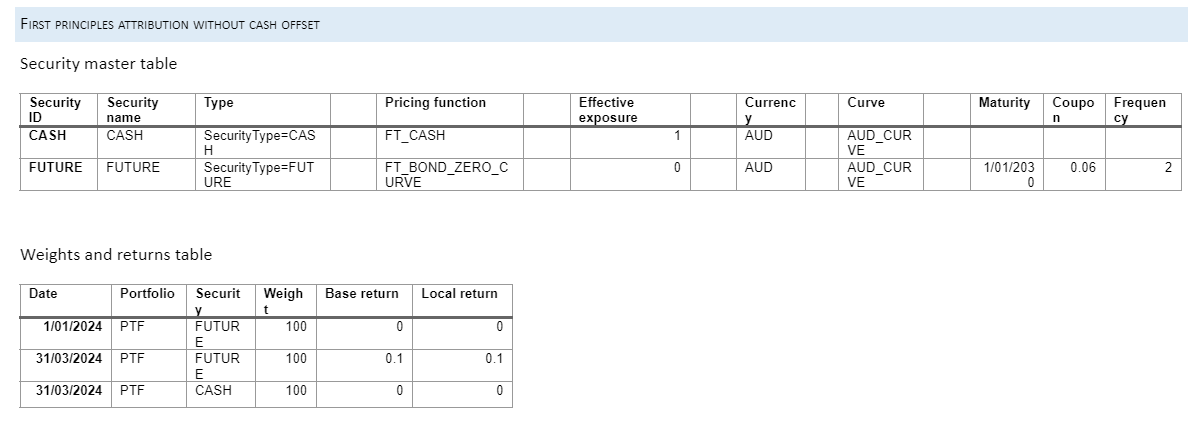
As this example uses first principles attribution, pricing functions are supplied for each security and no risk numbers are supplied in the weights and returns table. Maturity, coupon and frequency are provided for the bond instrument, which should be those of the current CTD for the futures contract. All effective exposures are set to 1 and a cash offset, with weight equal and opposite to that of the bond instrument, is supplied.

Notes

As in the previous example, pricing functions are supplied for each security and no risk numbers are supplied in the weights and returns table. Maturity, coupon and frequency are provided for the bond instrument, which should be those of the current CTD for the futures contract. 

The effective exposure of the bond instrument is set to 0 and no cash offset is used.

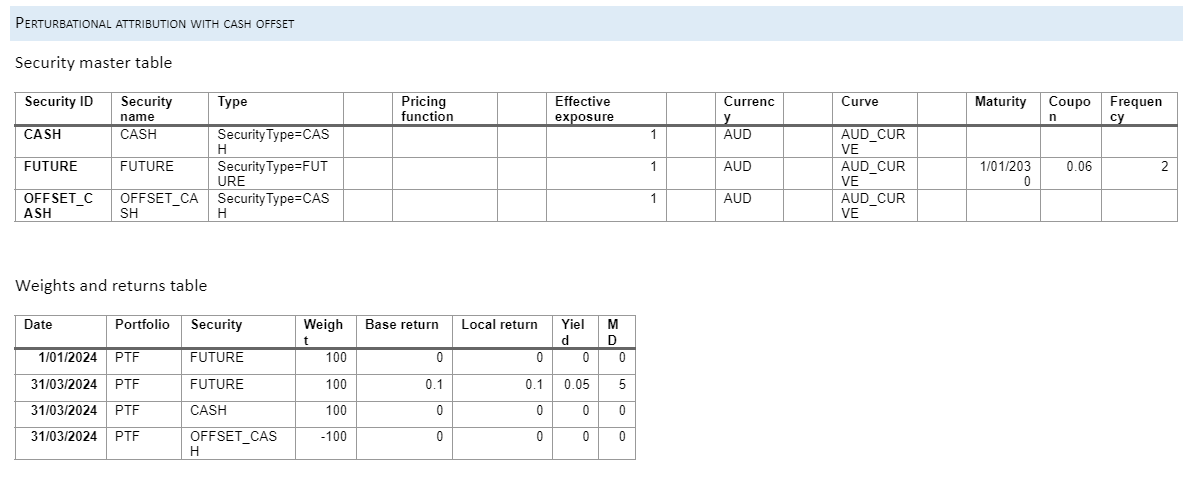
Notes

In this example, no pricing functions are supplied, so risk numbers are provided in the weights and returns table. 

Maturity, coupon and frequency are provided for the bond instrument, which should be those of the current CTD for the futures contract. The program does not need these to run the attribution calculation, but they may be used in reporting.

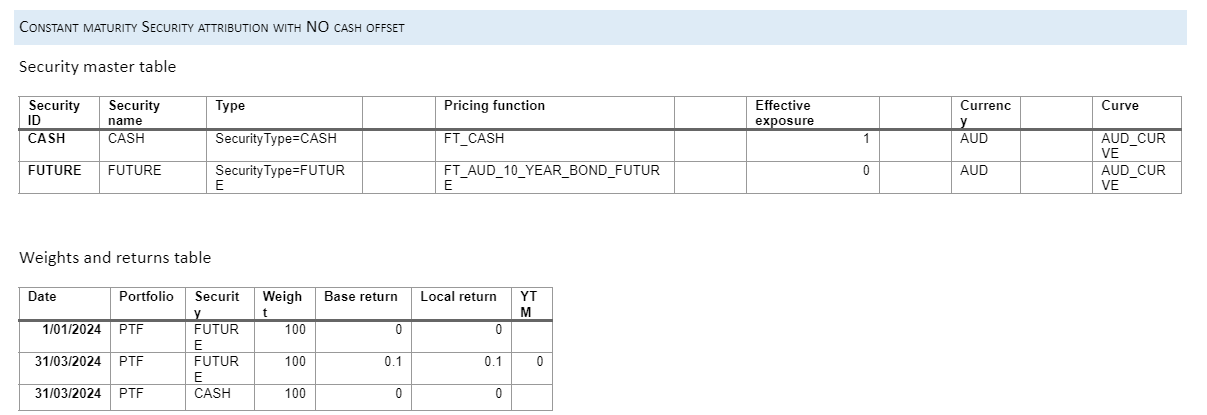
Notes

In this example, a pricing function for a 10 year bond future is supplied instead of a bond. This function does not require a maturity, coupon or frequency data, so these are not supplied.

The effective exposure of the bond instrument is set to 0 and no cash offset is used.

Note that we have set up an explicit YTM of zero, ensuring that carry return for this future is always zero. This supplied value will overwrite any internally calculated value.